🥽
OpenGL ES 3차원 컴퓨터그래픽스 수학
September 22, 2024
ⓒ 2019. JungHyun Han Korea University Seoul, All rights reserved.
Matrices and Vectors
m x n 벡터를 표현할 때, m = n 이면 정사각(square) 행렬이라 부른다.

A 행렬의 크기가 l x m 이고, B 행렬의 크기가 m x n 이면,
- A * B = l x n 행렬이 된다.

- OpenGL은 열벡터를 사용하고, M*V와 같이 행렬-벡터 (vector-on-the-right)곱셈을 사용하는 반면, Direct3D는 행벡터를 사용하고, V^T*M^T와 같은 방식(vector-on-the-left)을 사용한다.
Coordinate System and Basis
- Coordinate System = origin(원점) + basis(기저)
좌표계 = 공간
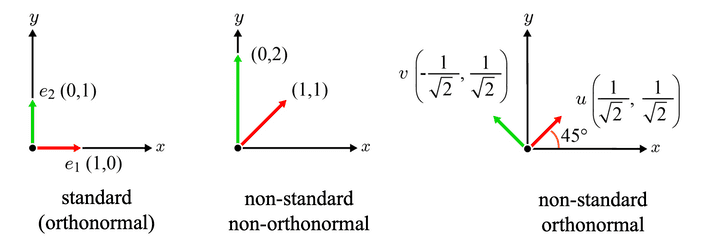
- 표준기저에서 보다싶이 e1과 e2가 주축 (principle axis, x축과 y축)에 나란하므로, e1과 e2를 특별히 표준기저(Standard Basis)라고 한다.
- 표준 기저는 linear combination을 통해, 2차원 공간의 모든 벡터를 표현할 수 있다.
- orthogonal + normalized = orthonormal standard
- non-orthogonal + non-standard(단위벡터가 아님) = non-orthonormal non-standard
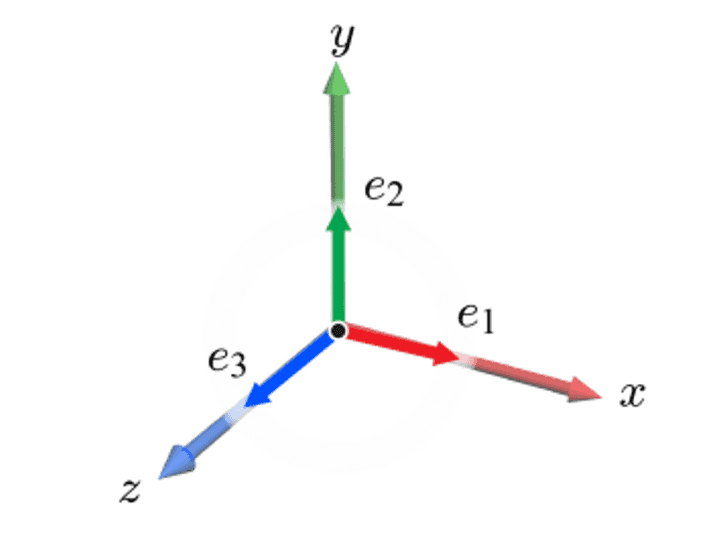
3차원에서의 좌표계
Line, Ray and Linear Interpolation
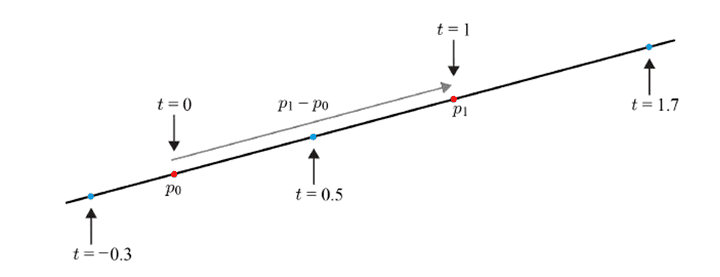
- p0와 p1을 잇는 벡터는 p1-p0를 사용하여 정의할 수 있다.
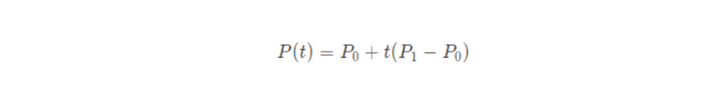
- t는 매개변수이고, 해당 공식은 매개변수 방정식이 되겠다.
- If
tis in [-∞, ∞], p(t) is an infinite line - when
tis restricted to [0, 1], p(t) represents the line segment, which corresponds to the linear interpolation of P0 and P1.- P0와 P1의 가중치값으로 생각해도 된다.
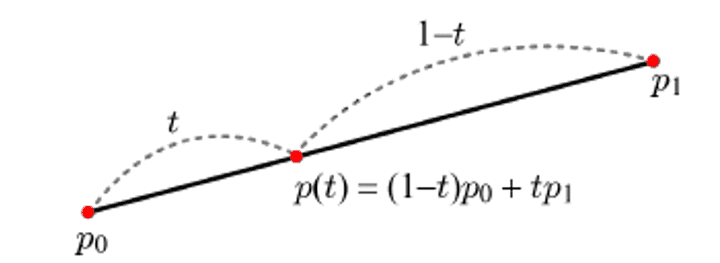
공간에서 선형보간으로 점의 좌표를 계산
- Linear interpolation in 3D space
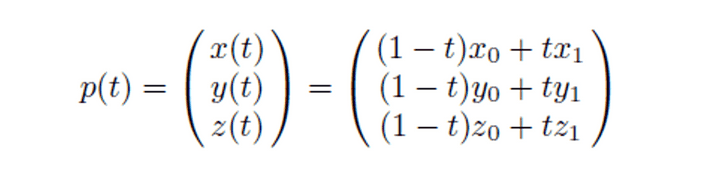
- 선형보간은 컴퓨터 그래픽스에서 매우 자주 나오는 개념이니 잘 숙지하자.
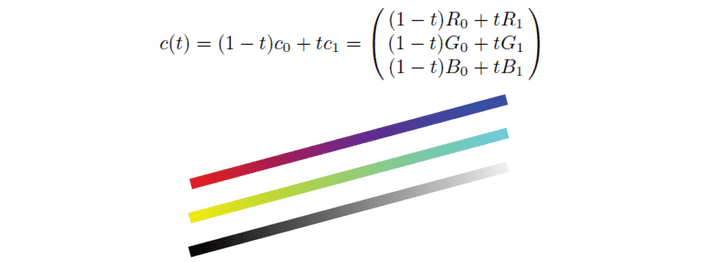 color linear interpolation
color linear interpolation