OpenGL ES 3차원 컴퓨터그래픽스 스케일링
ⓒ 2019. JungHyun Han Korea University Seoul, All rights reserved.
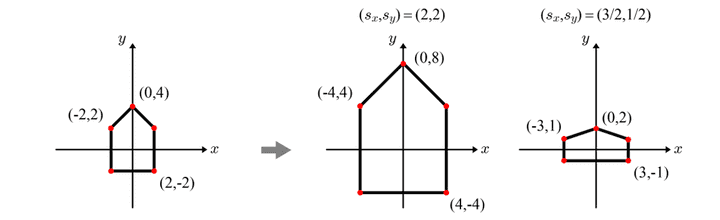
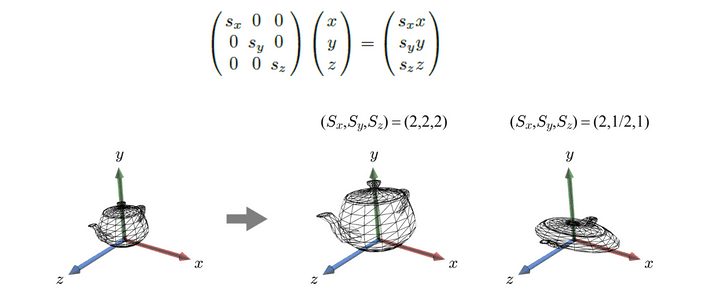
Scaling(축소/확대)
2차원 축소 확대는, x방향과 y방향인자를 포함하게 된다.
- 행렬의 곱셈으로 처리함
Rotation(회전 변환)
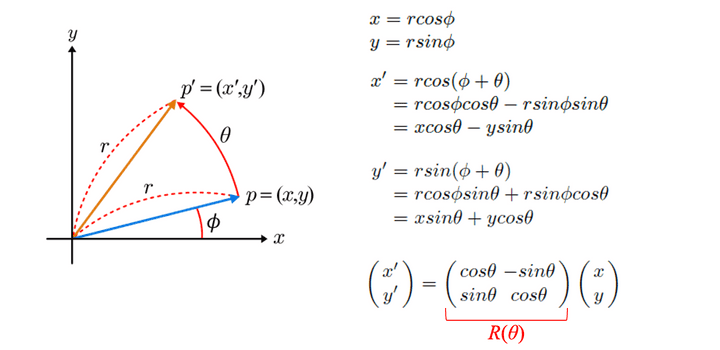
- 반시계/시계 방향은 사실 상관없음. 음수로 작성하면 동일하다.
Translation anf Homogenous Coordinates
주어진 x,y를 dx dy만큼 이동하는 것을 의미함.
- 벡터의 덧셈으로 정의됨.
동차좌표 (homogeneous coordinates)
회전 변환과 똑같이 벡터의 곱셈으로 나타냈으면 좋겠다.
(x, y) → (x, y, 1)
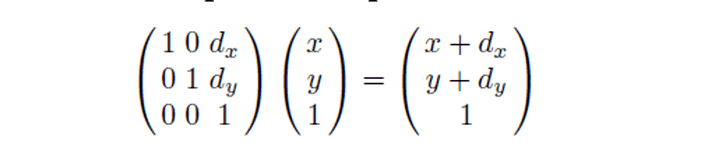
- scaling과 rotation과 다른 점은 3 x 3 행렬이라는 점.
사실 (x,y,1) 이라고 했지만, 꼭 1일 필요는 없다. with any non-zero w 가능하기 때문에, (wx, wy, w) 로 정의해도 괜찮다.
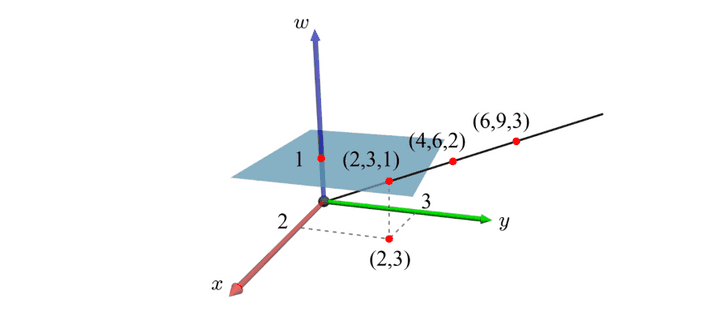
- 반대로 Cartesian 좌표를 변환하는 것은, w로 모든 요소를 나눠주면 될 것이다.
Scaling과 Rotation도 3x3좌표를 만들어야 하지 않을까?
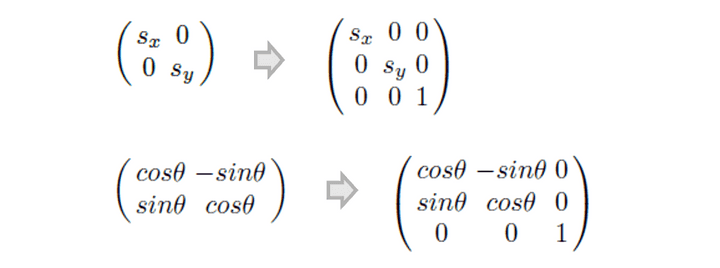
- 0 0 1 0 0을 추가하여 3차원으로 변환해주고, 계산하면 결과는 동일하다.
Multiple Transforms
Transform을 할 때에는 꼭 한가지 종류만 실행된다기보단, 여러가지가 같이 적용되는 경우가 많을 것이다.
- 이때는 따로따로 계산하는 것이 아니라, 순서에 맞춰서 행렬계산을 하면 될 것 같다.
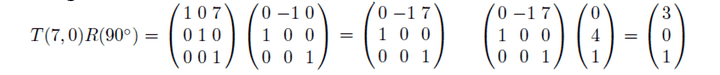
- 정말 중요한건,
교환 법칙이 성립하지 않는다는 점이다. 순서를 잘 고려하자!
원점이 아닌 중심으로?
사실 지금까지 본 케이스들은 모두 원점을 중심으로 생각해본 것이다. 우리가 생각해야할 것은, 임의의 점을 중심으로 할 때를 고려해보아야 하는 것이다.
- 원점으로 translation한다고 생각했을 때, 그때의 움직임을 계산한 후 다시 복구하는 방식이 될 것 같다.
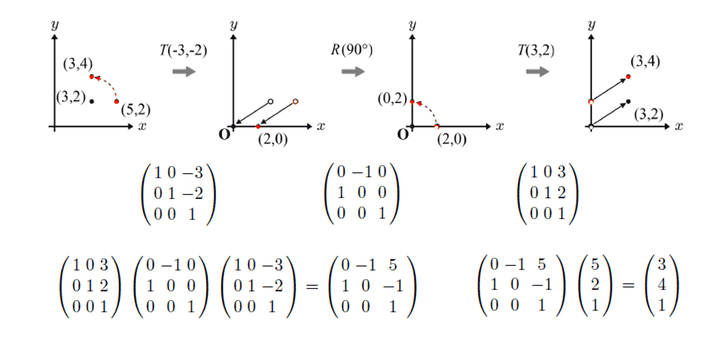
결국엔 모든 변환과정은 3x3 행렬들을 이용하기 때문에 나름 편하게 계산해볼 수 있을 것이다.
- Linear transform
- Scaling (S),
- Rotation (R),
- Translation (T)
1번과 2번을 나눈 이유는 밑에서 알게 될 것이다.
3x3행렬 결과값에서 맨 마지막 줄은 무시하면 되고, 결국 L파트와 t파트를 나누어 살펴볼 필요가 있을 것 같다.
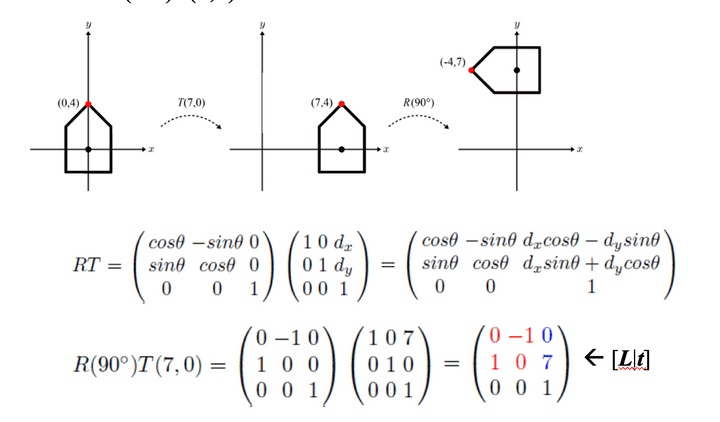
-
앞에 있는 2x2행렬만 L값으로 분류를 하는데, 이는 위의 1번에 해당하는 Linear Transform에 해당되는 변환만 계산된다. 즉, Translation은 계산되지 않은 채로 나온다.
-
t값의 경우 translation뿐만 아니라 linear transform에 해당되는 변환도 모두 계산된 채로 변환되는 것을 볼 수 있다.
즉, 순서를 다시 정리해보면,
- L이 선형변환을 먼저 적용이 된다.
- 해당 물체에 t를 적용한다.
Affine 변환은 수많이 들어올 수 있지만, 결국 형태는 [ L|t ] 형식으로 이루어진다.
- L|t 형식 안의 L에서 Scaling 변환이 빠진 형태를
R|t라고도 한다. - 스케일링이 빠진 거 외에는 따로 바뀐 것이 없기 때문에 기존의 L|t 변환과 성질은 동일함.
How about 3D?
3D Rotation
2D Rotation과 다르게, 3D Rotation에서는 축을 중심으로 회전을 하게 된다.
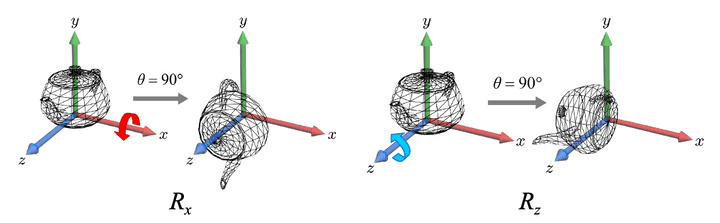
Z-axis (Rz)
Obviously, z’=z.
z축을 기준으로 회전하기 때문에, z좌표의 변화는 없다.
- 다만, 나머지 다른 x,y좌표들은 2차원 rotation과 같은 원리로 움직인다고 생각하면 된다.
X-axis (Rx)
Obviously, x’=x. 눈을 x축에 두고 본다면, Rz일 때 x축이 y축이되고, Rz일 때 y축이 z축이 되어 같은 원리로 작동한다는 것을 알 수 있다.
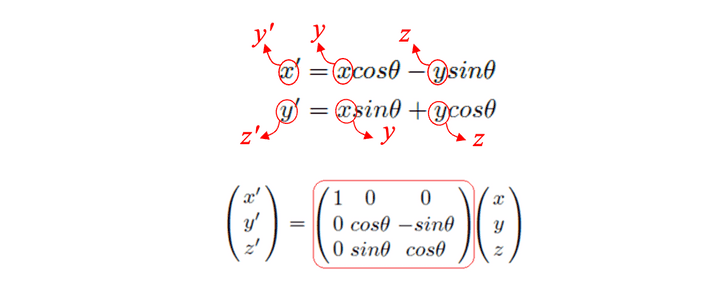
Y-axis (Ry)
같은 원리로 동일하게 작동한다.
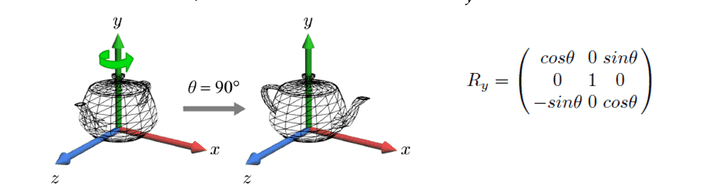
모든 축을 중심으로 회전을 한다고 할 때,
- Counter-Clock Wise라면 각도는 양수를 사용하면 되고,
- Clock wise라면, 각도는 음수를 사용할 수 있을 것이다.
3D Translation
2D에서는 3x3 행렬을 사용했다면, 여기서는 3x3에 하나를 더 추가한 4x4 행렬을 사용해서 변환을 한다.
- 지금까지 해왔던 3x3 행렬들도 같이 계산될 수 잇도록 4x4행렬로 바꿔줘야한다.
World Transformation
좌표계는 하나의 물제를 기준으로 만들어진 object space를 기준으로 만들어지는데, 각각의 object space를 게임과 같은 하나의 환경으로 묶어야 할 것이다. 이 하나의 환경을 world space라고 칭하고,
-
object space에서 world space로 변환하는 행위가 바로 앞에서 우리가 계속 배운 transform (더 자세하게는 world transform)의 형태가 되겠다.
-
교환법칙은 당연히 성립안됨. -
L|t 형식 또한 그대로 유지됨 (3D에서는 3x3이 L의 형태가 되겠다.)
-
똑같이 L 먼저 → t 나중. 같은 원리이다.
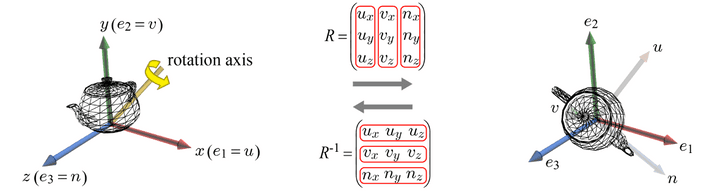
Rotation and Object-space Basis
모든 transform이 끝나고 조정이 된 이후에는, 모든 정점들이 다 고정점이 될 것이다. 이를 object space에 딱 붙어있다 로 이해하면 될 듯?
- (os = ws) 물체가 회전하면, object space의 basis는 물체와 고정되어 있기 때문에 같이 회전하게 된다.
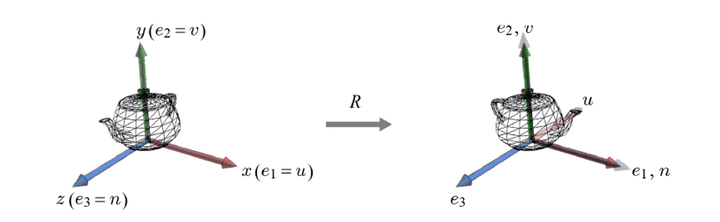
- u, v, n이라는 벡터를 바탕으로 방향을 설명할 수 있다.
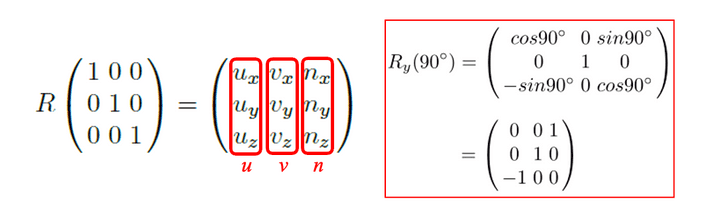 u,v,n 세 벡터를 합친 행렬이 결국 I행렬이라는 걸 알 수 있다.
u,v,n 세 벡터를 합친 행렬이 결국 I행렬이라는 걸 알 수 있다.
R’s columns are u, v, and n. Given the ‘rotated’ object-space basis, {u, v, n}, the rotation matrix is immediately determined, and vice versa.
방향을 바로 알 수 있다!!
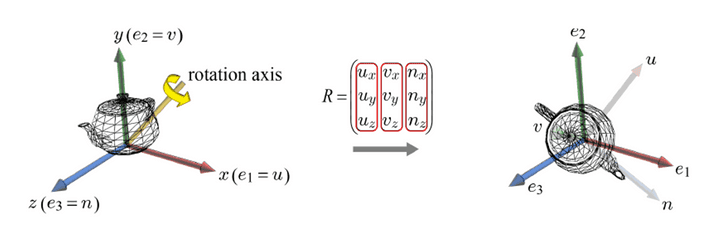
- 이런 임의의 축에 적용할 때에도, u, v, n의 어떻게든 알게 되었다면, 바로 방향을 알 수 있다.
Inverses of Translation and Scaling
이전에 했던 변환을 무효화 시키는 것이, 역변환의 가장 큰 목적이다.

Inverse Rotation
앞에서 봤던, u,v,n 벡터들은 각각 단위가 1인 단위벡터이고 세 개중에 어느 쌍을 고르던 orthonormal하다.
- 서로 각각을 내적을 하면 0인 점도 당연히 알 수 있다.
- Transpose가 핵심 개념이 되겠다.
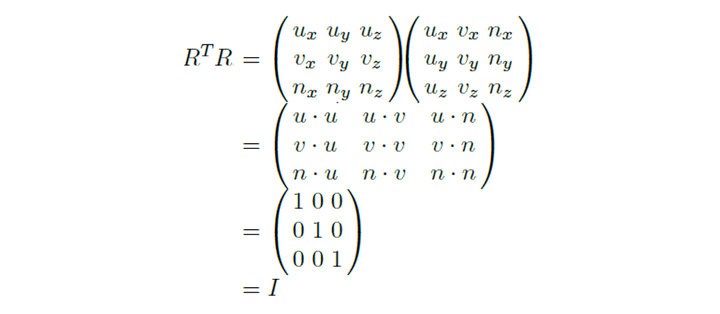 u, v, and n form the columns of R, they form the rows of R-1
u, v, and n form the columns of R, they form the rows of R-1
- e1, e2, e3와 나란하게 원상복구하고 싶다면, u,v,n을 행으로 쌓은 역변환 행렬을 적용해주면 바로 찾을 수 있다는 것이다.